Eine hochinteressante, neue Eigenschaft in CSS3 ist transform. Sie ermöglicht lineare Transformationen beliebiger Seitenelemente, d.h. wir können sie verschieben, rotieren, skalieren und scheren. Auf den ersten Blick wirkt das Konzept recht kompliziert und mag so manchen abschrecken, der von Vektoren und Matrizen Ausschlag bekommt. In Wirklichkeit ist es aber gar nicht so kompliziert, zumal es gesonderte Funktionen gibt, die sich intuitiv nutzen lassen, und die die Matrix vor den Augen des Designers verbergen. Auch diese neue Eigenschaft wird von allen modernen Browsern, abgesehen vom IE, bereits unterstützt.
Definition
Die transform-Eigenschaft ist eigentlich recht simpel:
<transform> =
none|<transform-function>[ <transform-function>]*
Der Standardwert ist schlicht none, es wird also keine Transformation durchgeführt. Alternativ kann eine einzelne oder eine Folge von beliebig vielen Transformationsfunktionen angegeben werden, die entsprechend ihrer Reihenfolge durchgeführt werden.
Zusätzlich existiert eine zweite Eigenschaft namens transform-origin. Sie definiert, wo der Ursprung des zu transformierenden Objektes liegt. Dies ist beispielsweise bei Rotationen interessant, da es einen Unterschied macht, ob ich ein Objekt um sich selbst (Ursprung = der eigene Mittelpunkt) drehe, oder es auf die Umlaufbahn um ein anderes Objekt schicke (Ursprung = Mittelpunkt der Umlaufbahn). Unverständlich? Dann hilft ein Blick auf das Beispiel zur Rotation und das anschließende Beispiel zum versetzten Ursprung.
Standardmäßig ist der Ursprung immer der Mittelpunkt des zu transformierenden Objektes. transform-origin ist wie folgt definiert:
<transform-origin>=
[[<percentage>|<length>|left|center|right] [<percentage>|<length>|top|center|bottom]?] |
[[left|center|right] || [top|center|bottom]]
Der Ursprung kann also aus einer Prozent/Länge/Keyword-Kombination definiert werden, z.B. 50% 50% für den Mittelpunkt, 0 0 für die linke, obere Ecke oder right bottom für die untere, rechte Ecke. Wird nur ein Wert angegeben, wird der zweite Wert als center angenommen. Der erste Wert steht jeweils für die horizontale und der zweite Wert für die vertikale Richtung, wobei bei Verwendung von zwei Keywords die Reihenfolge auch geändert werden kann, da sich die Ausrichtung dann aus den Keywords ergibt.
Funktionen und Parameter
Wie zuvor erwähnt, erhält die transform-Eigenschaft nicht einfach nur ein paar Parameter, sondern verschiedene Funktionen, die der Reihe nach abgearbeitet werden. In diesem Abschnitt werde ich die matrix-Funktion genauer erläutern und auf die weiteren kurz eingehen. Die anschließende Sektion Beispiele zeigt die einzelnen Funktionen dann im Einsatz.
matrix(<number>,<number>,<number>,<number>,<number>,<number>)
matrix ist sozusagen die Mutter aller Transformationsfunktionen. Mit ihr lassen sich alle folgenden Funktionen und deren Kombinationen in einer einzelnen Funktion abbilden. Das ist nicht so intuitiv und lesbar, wie es die Verwendung der anderen Funktionen wäre, kann aber gerade bei komplexen Funktionsfolgen deutlich kürzer und bei dynamischen Variationen (z.B. via JavaScript) praktischer sein. Wem die Matrixschreibweise zu kompliziert ist, der kann auch direkt zu den anderen Funktionen springen. Ich bemühe mich, alles einigermaßen verständlich zu erklären, auch wenn dabei möglicherweise die mathematische Genauigkeit ein wenig verloren geht. Anschließend gibt es aber noch ein paar Links zur Vertiefung im Detail 😉
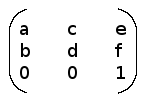Alle Transformationen können mit einer 3×3-Matrix dargestellt werden, wie in der rechten Abbildung zu sehen ist. Da die letzte Zeile konstant ist, müssen wir der Matrixfunktion nur 6 Parameter übergeben: matrix(a,b,c,d,e,f). Eine solche Matrix definiert den Unterschied von einem neuen Koordinatensystem zum ursprünglichen Koordinatensystem. Unser Objekt wird also in ein neues Koordinatensystem übertragen. Die einfachste Abbildung ist diejenige, die nichts verändert: matrix(1,0,0,1,0,0). e und f ermöglichen es uns, unser Objekt zu verschieben (Translation). Setzen wir z.B. jeweils 10px ein, dann verschieben wir das Objekt 10 Pixel nach rechts und 10 Pixel nach unten, ändern es aber sonst nicht: matrix(1,0,0,1,10px,10px). Für die anderen Transformationen sieht es so aus:
- Scaling via Matrix: matrix(x,0,0,y,0,0)
Mit x definieren wir die Skalierung in der x-Achse (Breite) und mit y in der y-Achse (Höhe). Setzen wir x z.B. auf 2, dann verdoppeln wir die Breite, setzen wir y auf 0.5, dann halbieren wir die Höhe. - Rotation via Matrix: matrix(cos(x), sin(x), -sin(x), cos(x), 0, 0)
Hier entspricht x dem Winkel der Rotation. Wollen wir unser Objekt um den Winkel x=90° drehen, dann wäre der Funktionsaufruf matrix(0,1,-1,0,0,0). - Skew X via Matrix: matrix(1, 0, tan(x), 1, 0, 0)
Skew Y via Matrix: matrix(1, tan(x), 0, 1, 0, 0)
Auch beim Scheren brauchen wir einen Winkel. Dieser beschreibt, wie sich die zu verändernde Achse im Verhältnis zur anderen Achse bewegen soll. Daher auch der Begriff „scheren“: wir klappen die Achsen des Koordinatensystems wie eine Schere zusammen bzw. auseinander. Wollen wir um 45° längs der x-Achse scheren, dann wäre der Aufruf matrix(1, 0, 1, 1, 0, 0), d.h. wir drehen die x-Achse um 45° auf die y-Achse zu.
Wollen wir mehrere Transformationen hintereinander mit einer Matrix ausführen, dann müssen wir die Matrizen miteinander multiplizieren. Die Ergebnismatrix ist dann sozusagen unser all-inclusive-Paket, wie man beim Beispiel zur Kombination von Funktionen sehen kann. Um diesen Schritt etwas zu vereinfachen, habe ich einen CSS3 transform Matrizenrechner zusammengebaut. Damit könnt ihr Transformationsmatrizen miteinander multiplizieren, einzelne Funktionen auf eure Matrix anwenden, ein Beispiel ansehen (sofern es in das Sichtfeld passt ;)) und auch die Rechenschritte beim Multiplizieren der Matrizen nachvollziehen.
Hier noch ein paar weiterführende Links, bevor wir uns den einfacheren Alias-Funktionen zuwenden:
- Definition der Transformationsmatrix beim W3C
- Wikipedia: Lineare Transformationen
- Wikipedia: Matrizenmultiplikation
translate(<translation-value>[,<translation-value>])
Translate verschiebt das Objekt entsprechend des angegebenen Längenwertes (z.B. 10px). Der erste Wert bezieht sich auf die x-Achse (horizontal), der zweite Wert auf die y-Achse (vertikal). Wird der zweite Wert nicht angegeben, wird 0 angenommen. Alternativ kann mit translateX(<translation-value>) bzw. translateY(<translation-value>) direkt ein Wert für Verschiebung auf der x- bzw. y-Achse angegeben werden. (Somit sind translate(<translation-value>) und translateX(<translation-value>) synonym.) [Beispiel]
scale(<number>[,<number>])
Skaliert das Objekt um den numerischen Wert, also z.B. 2 für die doppelte und 0.5 für die halbe Größe. Der erste Wert bezieht sich auf die x-Achse (horizontal), der zweite auf die y-Achse (vertikal). Wird nur der erste Parameter angegeben, wird der Wert für beide Achsen verwendet. Alternativ kann mit scaleX(<number>) oder scaleY(<number>) eine Achse auch direkt verändert werden. [Beispiel]
rotate(<angle>)
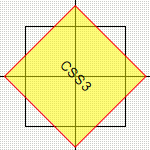
Dreht das Objekt gemäß dem angegebenen Winkel um den Ursprung. Winkel werden als Zahl + deg geschrieben, also wäre der Parameter 90deg für eine Rotation um 90°. [Beispiel]
skew(<angle>[,<angle>])
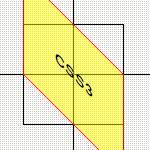
Schert das Objekt. Auch hier sind Winkelangaben (Zahl + deg, also z.B. 90deg für 90°) notwendig. Der erste Wert steht für die Scherung zur x-Achse, der zweite Wert für die Scherung zur y-Achse. Wird nur der erste Wert angegeben, wird für die y-Achse 0° (= keine Änderung) angenommen. Alternativ gibt es skewX(<angle>) bzw. skewY(<angle>), um gezielt eine Achse anzusprechen. [Beispiel]
Solange sich die Eigenschaft noch in Entwicklung befindet, verwenden Webkit- und Mozilla-Browser ein Präfix. Möchte man sie bereits verwenden, muss sie daher mehrfach mit gleichen Parametern definiert werden: transform[-origin] (Opera), -moz-transform[-origin] (Mozilla) und -webkit-transform[-origin] (Webkit).
Beispiele
Die folgenden Beispiele werden an einem 50% transparenten, gelben DIV-Element mit rotem Rahmen gezeigt. Im Zentrum des DIV-Elements steht zudem der einfache Text CSS3. Zum besseren Verständnis befindet sich im Hintergrund ein Koordinatensystem, dass zusätzlich durch einen schwarzen Rahmen die Ursprungsform des DIV-Elements zeigt. So sieht das ganze ohne Transformationen aus (der schwarze Ursprungsrahmen ist hier natürlich nicht zu sehen):
| Live-Demo |
|---|
|
CSS3
|
Für eigene Experimente eignet sich der CSS3 transform Matrizenrechner.
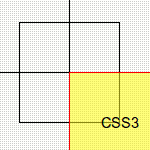
Bei der Translation handelt es sich um die einfachste Form der Transformation. Das Objekt wird einfach innerhalb des Koordinatensystems verschoben. Eine Translation kann folgendermaßen definiert werden:
[cc lang=“css“]
/* Variante 1: Matrix */
transform:matrix(1, 0, 0, 1, 50px, 50px);
/* Variante 2: Translate */
transform:translate(50px, 50px);
/* Variante 3: TranslateX und TranslateY */
transform:translateX(50px); /* entspricht translate(50px); */
transform:translateY(50px);
[/cc]
| Live-Demo |
|---|
|
CSS3
|
Bei einer Rotation wird das Objekt einem Winkel entsprechend um den Ursprung gedreht. Per Default liegt der Ursprung in der Mitte des Objektes:
[cc lang=“css“]
/* Variante 1: Matrix
matrix(cos(45°), sin(45°), -sin(45°), cos(45°), 0, 0) */
transform:matrix(0.7, 0.7, -0.7, 0.7, 0, 0);
/* Variante 2: Rotate */
transform:rotate(45deg);
[/cc]
| Live-Demo |
|---|
|
CSS3
|
Am Beispiel der Rotation kann die Eigenschaft transform-origin schön demonstriert werden. Eigentlich gilt der Mittelpunkt des Objektes als Ursprung, aber mit transform-origin kann er beliebig verschoben werden. Das folgende Beispiel zeigt rotate mit den gleichen Parametern, wie sie in Beispiel 2 gesetzt waren, verschiebt aber den Ursprung von der Mitte in die linke, obere Ecke des Objektes:
[cc lang=“css“]
/* Variante 1: Prozent */
transform-origin:0% 0%;
/* Variante 2: Längenangaben */
transform-origin:0 0;
/* Variante 3: Konstanten */
transform-origin:top left;
[/cc]
| Live-Demo |
|---|
|
CSS3
|
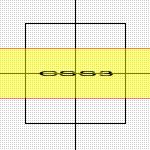
Scaling ermöglicht es uns, unser Objekt in die x- bzw. y-Richtung zu skalieren, also zu verkleinern oder zu vergößern. Im Beispiel wird die Höhe halbiert und die Breite verdoppelt:
[cc lang=“css“]
/* Variante 1: Matrix */
transform:matrix(2, 0, 0, 0.5, 0, 0);
/* Variante 2: Scale */
transform:scale(2, 0.5);
/* Variante 3: ScaleX und ScaleY */
transform:scaleX(2); /* entspricht scale(2,1); */
transform:scaleY(0.5);
[/cc]
| Live-Demo |
|---|
|
CSS3
|
Mit Skew können wir unser Objekt längs seiner x- bzw. y-Achse scheren. Im Beispiel wird um 45° längs der y-Achse verzerrt:
[cc lang=“css“]
/* Variante 1: Matrix
matrix(1, tan(45°), tan(0°), 1, 0, 0)
*/
transform:matrix(1, 1, 0, 1, 0, 0);
/* Variante 2: Skew */
transform:skew(0deg, 45deg);
/* Variante 3: SkewX und SkewY */
/* transform:skewX(0deg); — in diesem Fall unnötig,
entspricht skew(0deg,0deg); */
transform:skewY(45deg);
[/cc]
| Live-Demo |
|---|
|
CSS3
|
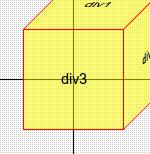
Natürlich können wir die einzelnen Funktionen auch kombinieren – entweder in einer Matrix, oder eben durch Hintereinanderausführen der Funktionen:
[cc lang=“css“]
/* Variante 1: Matrix */
.div1 {transform:matrix(1, 0, -0.5, 0.5, 25px, 26px)}
.div2 {transform:matrix(0.5, -0.5, 0, 1, 75px, -25px)}
.div3 {transform:matrix(1, 0, 0, 1, 0, -101px)}
/* Variante 2: Einzelfunktionen */
.div1 {transform:translate(25px,26px) skewX(-45deg) scaleY(0.5)}
.div2 {transform:translate(75px,-25px) skewY(-45deg) scaleX(0.5)}
.div3 {translateY(-101px)}
[/cc]
| Live-Demo |
|---|
|
div1
div2
div3
|