Weiter geht es mit der Reihe über die Gestaltgesetze. In dieser Folge wird das Gesetz der Kontinuität näher erläutert, wobei hier auch begriffliche Unschärfen erkennbar sind. Denn einige Teile dessen, was nun erläutert wird, findet sich anderswo auch unter den Namen Gesetz der guten Fortsetzung, Gesetz der fortgesetzt durchgehenden Linie, Gesetz der fortgesetzten Form oder ist gar bereits unter Good Shape (Prägnanz).
An diesem Begriffsproblem möchte ich mich aber nicht allzu lange aufhalten. Mittlerweile zählt man mehr als 100 Gestaltgesetze, sodass Überschneidungen und Unschärfen kaum auszuschließen sind. Sicherlich ist die unterschiedliche Einordnung von Problemen auch darauf zurückzuführen, dass die Gesetze in verschiedensten Disziplinen vom Mediengestalter bis zum Psychologen verwendet werden. Da hier die Auswirkungen, die die Gesetze in Bezug auf die Wahrnehmung beschreiben, erläutert und daraus Konsequenzen für mögliche Umsetzungen im Web- oder Screen-Design gezogen werden sollen, habe ich mich hier für die zusammengefasste Variante entschieden.
Schauen wir uns zuerst das Bild am Artikelanfang an. Wir können den Würfel problemlos erkennen, obwohl er eigentlich gar nicht da ist. Innerhalb der Kreise werden Ecken angedeutet, die wir automatisch entsprechend fortsetzen und so die fehlenden Kanten des Würfels erkennen können.
Das nebenstehende Bild zeigt zwei einzelne Linien. (Mancher mag jetzt darauf hinweisen, dass er ein A erkennt. Dies ist auf das Gesetz der Erfahrung zurückzuführen, das in einem späteren Artikel behandelt wird.) Wir gehen direkt davon aus, dass es sich um eine gerade Linie und um einen Bogen handelt, d.h. wir schließen die Möglichkeit, dass die Linien an den Kreuzungspunkten „abbiegen“, aus und verlassen uns auf die kontinuierliche Fortsetzung. Daraus können wir einige Schlußfolgerungen für die Gestaltung von Grafiken ziehen, wie das folgende Beispiel anhand eines Diagramms zeigen soll.
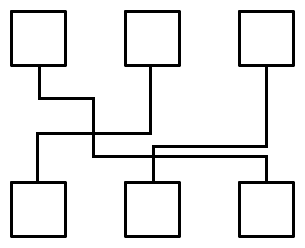Links sehen wir nun ein ganz einfaches Diagramm, das Verbindungen von jeweils einem oberen Kästchen zu einem der unteren Kästchen aufzeigt.
Obwohl es keinerlei Hinweise auf die Forsetzung der Pfade an den Schnittpunkten gibt (z.B. kurze Unterbrechungen eines Pfades oder kleine Bögen um ein „übersteigen“ anzudeuten), können wir sie sehr gut nachvollziehen, da wir Richtungsänderungen an diesen Stellen ausschließen. Dennoch kann es notwendig sein, dass wir durch die vielen Verzweigungen der Einzelpfade erst genauer hinsehen müssen, bevor wir die Zusammenhänge klar erfasst haben. Die tatsächlichen Wege lassen sich einfach nicht auf den ersten Blick erfassen, zumal auch teilweise die Nähe einzelner Linien zueinander Verwechslungen provozieren kann. Aber auch dafür gibt es Abhilfe, wie das nächste Bild zeigt:
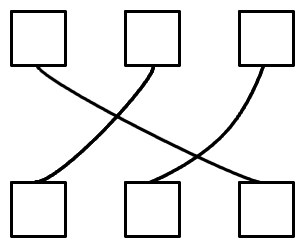Hier wird genau der gleiche Inhalt aus dem vorhergehenden Bild gezeigt, d.h. die Pfade verbinden hier die gleichen Ausgangsquadrate. Es fällt aber deutlich leichter, die Pfade auf den ersten Blick zu erkennen und so die Quadrate direkt zuzuordnen.
In dieser Variante bewegen sich die Pfade direkt auf ihr jeweiliges Ziel zu. Sie sind zwar leicht geschwungen, knicken aber nicht in verschiedene Richtungen ab. Dadurch wird es überflüssig die Pfade zum Verständnis erst nachvollziehen zu müssen. An den Schnittpunkten bleibt die Fortsetzung der Wege nach wie vor klar bzw. ist vermutlich sogar noch deutlicher, da die Fortbewegung durch die Krümmungen gut differenziert werden können und keine Verwechslungen durch nahe beieinander fortlaufende Pfade provoziert werden.
Bei der Gestaltung von Pfaden und anderer Linien können wir dank der Kontinuität unter Berücksichtigung der anderen Gesetze (z.B. Nähe) die Lesbarkeit der Grafik für den Betrachter stark verbessern.
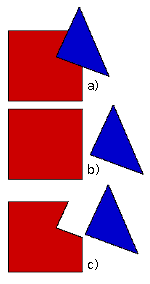Das Gesetz der Kontinuität bezieht sich aber nicht nur auf die Fortsetzung von einfachen Linien, sondern ebenfalls auf komplexere Elemente. In der nebenstehenden Grafik sehen wir unter a) eine rote Form und ein blaues Dreieck. Da das Dreieck die blaue Form überschneidet und somit teilweise verdeckt, können wir eigentlich keine Aussage über die tatsächliche Form des roten Bereichs machen.
Wir wissen aber dank des Gesetzes des Prägnanz, dass wir Objekte in möglichst klaren, einfachen Formen wahrnehmen. Hierbei hilft uns das Gesetz der Kontinuität, denn wir können die Außenlinien der roten Form in Gedanken fortführen, wodurch ein Quadrat entsteht, was wiederum der Vorstellung einer klaren Form entspricht. Beim Betrachten von a) erwarten wir also, dass es sich um die unter b) gezeigten Formen handelt, sobald man sie auseinanderzieht. Mit einem Ergebnis c) (oder gar einer ganz unerwarteten Fortführung, z.B. einer Rundung oder einer gezackten Linie) rechnen wir entgegen unter normalen Umständen nicht.
Diese Erkenntnis können wir in der Bildbearbeitung, aber auch bei der Oberflächengestaltung durchaus gebrauchen. Wir müssen immer dann, wenn sich Elemente überschneiden statt klar abgegrenzt nebeneinander zu stehen, damit rechnen, dass der Betrachter den verborgenen Bereich automatisch ergänzt und so auch eine gewisse Erwartungshaltung an den Tag legt. Schauen wir uns einfach folgenden (zugegeben recht konstruierten) Bildausschnitt an:
Das Fenster („Ungespeichertes Dokument 1 – gedit„) verdeckt hier einen Teil der Toolbar des darunterliegenden Fensters. Ein Nuter würde in diesem Fall mit großer Wahrscheinlichkeit erwarten, dass die Toolbar hinter dem Fenster weiterläuft, sich dort also weitere Ordner oder Symbole verbergen. Wäre dies nun die Default-Oberfläche eines einzelnen Programms, würde er sicher verwirrt sein, wenn die Toolbar hinter dem Fenster leer wäre. Sinnvoller wäre es augenscheinlich, die Toolbar z.B. komplett linksbündig anzuordnen, ihr rechts einen klaren Abschluss zu spendieren und das zusätzliche Fenster neben ihr zu positionieren. Schon würden wir beim Benutzer keine Erwartungen wecken, die wir nicht erfüllen können 🙂
Bildquelle Teaserbild „Würfel ohne Kanten“: Urheber Bernard Ladenthin, Quelle Wikipedia, gemeinfrei.
